正八面体と正四面体の体積比をカッコよく求める

辺の長さが1の正八面体と正四面体があるとします。

雰囲気的に正八面体の方が大きいのは明らかですが、具体的に正八面体の体積は正四面体の体積の何倍でしょうか？ もちろんそれぞれ計算して比をとれば良いのですが、カッコよい解き方があるので記しておきます。

積み木で遊ぶ

ややこしい計算はだるいので、以下のような正四面体積み木で遊びましょう。

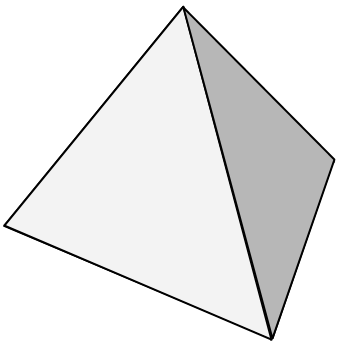
4つ積んでみます。

なにやら一辺の長さが2倍の正四面体ができました。よく見てみましょう。

…真ん中の空白は正八面体！

計算

先ほどの図

を見ると、

すなわち

一辺が2の正四面体 = 一辺が1の正四面体が4つ + 一辺が1の正八面体が1つ

一辺が1の正四面体の体積をVとすれば、一辺が2の正四面体の体積は2の3乗倍となる8Vなので、上の関係より

となります。これより、正八面体の体積は正四面体の4倍であることが分かりました。
積み木ってすごい。

多面体のおもちゃを紙でつくって遊んでいたときに思い出したので、ここに書いておきました。