現代美術館の展示を数学的に解説【ガブリエル・オロスコ展】
はじめに
(この記事は、現代アートの幾何学的な作品を理系的な目線から分析してみようと試みたものです。)
この前の週末に、東京都現代美術館で開催中の「ガブリエル・オロスコ展-内なる複数のサイクル」に行ってきました。
上記の公式Webサイトでは卓球台や車の展示写真が紹介されているのですが、正直言ってそれらの写真やポスターからは何の魅力も感じていなかったんですね。それにも関わらずダメもとで行ってみた*1ところ、これが面白かったのです。ガブリエル・オロスコはたぶん「かたち」に大きな関心を寄せていて、そのあたりが私の個人的な興味に合致していたみたいです。
作品を普通に解説してもおもしろくないので、ここではちょっとした数学(ほぼ算数)を使って彼の作品を紐解いていきましょう。
「サムライ・ツリー」
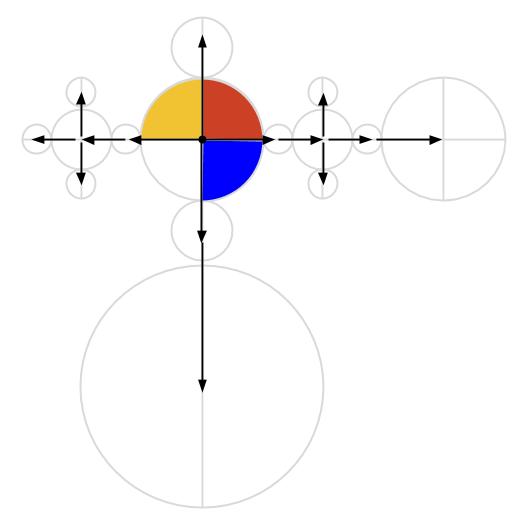
以下では、展示されていた作品のうち「Samurai Tree (サムライ・ツリー)」というものに注目します。撮影OKだったので、実際の写真を以下に載せました。

なんとなくモンドリアンの絵を思わせるような幾何学的な絵です。
サムライ・ツリーはどのように描かれたか?
この絵は以下のような方法に基づいて描かれています。
〈サムライ・ツリー〉のシリーズはすべて、中心の点から一つの円を描き、それを4分割した線の延長線上に次の円を隣接させ分割するという方法を繰り返して作られた同じ図から成ります。そこに赤・青・白・金の4色を斜め2マス先に進めるというチェスのナイトの法則に従い、配色していきます。ルールに従って自動的に出来上がるこのシリーズは、コンピュータを使って672種類の色違いの図が作られています。
(会場配布資料より引用)
このように、まずは中心から円を描き、それをナイトの法則に従って4色で塗り分けていることが分かります。特にジェネラティブアートやセルオートマトンが好きな人にはグッとくるかもしれないですね。
この文章だけではイメージしづらいかもしれないので、図を使ってもう少し詳しく説明しましょう。
1. 輪郭
中心の点から一つの円を描き、それを4分割した線の延長線上に次の円を隣接させ分割するという方法を繰り返して
という方法により、以下のような輪郭を描くことができます。上下左右に円をどんどん付け足していく感じでしょう。同様の方法を用いれば、これ以外の輪郭を独自に生成することもできそうですね。

(↑がんばって自分で描きました。疲れた…)
2. 塗り分け
上記の輪郭によって分けられた領域を、以下のように塗り分けていきます。
赤・青・白・金の4色を斜め2マス先に進めるというチェスのナイトの法則に従い、配色していきます
まずは以下のように中心の円を4色で塗り分けてみましょう。

ここさえ塗り分けてしまえば、あとは「チェスのナイトの法則」によって全ての円内の領域(背景除く)の色が定まります。
ナイトの法則なるものを具体的に言うと、「縦1+横2」または「縦2+横1」だけ離れた領域を同じ色で塗り分けるということです(下図)。

あとは背景を塗ればサムライ・ツリーの完成です。
構造:どこがツリーなのか
さて、この「サムライ・ツリー」という題ですが、どこがサムライなのかよくわからないし、ツリー(木)に似ているわけでもありません。ただ、この絵のどこにツリーと呼ばれる所以があるかということには気がつきました。そのことを説明します。
前提知識:木構造
木構造と呼ばれるデータ構造があります(下図)。
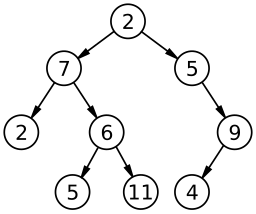
木構造 (データ構造) - Wikipedia
木構造はノード(頂点)とエッジ(ノード間を結ぶ辺)で表されるデータ構造であり、家系図のようなものですね。上図の一番上が「根ノード(root node)」であり、そこから「子ノード(child node)」へと枝分かれしています。
配色:なぜ672通りなのか
サムライ・ツリーの形状が木構造になっていることが分かりました。今度は色分けに注目しましょう。
赤・青・白・金の4色で塗り分けられていますが、すでに引用した会場配布資料によれば672種類の色違いが存在するそうです。672って7の倍数だし、一体どう計算したら672種類になるの?と思ったので、計算してみました。
中心の円(4等分)の塗り分け方
中心に存在する4等分された円は、必ず赤・青・白・金の4色で塗り分けます(下図)。

この塗り分け方、つまり中心の円の右上・左上・左下・右下を異なる4色で塗り分ける方法は、高校数学の知識によれば 4! = 24通り存在しますね。
その他の円の塗り分け方
すでに紹介した「ルール(チェスのナイトの法則に基づいた塗り分け方)」によると、中心の円の色分けを決めれば、他の円内の各領域の色は一意に決まります。
したがって、すべての円の領域内の塗り分け方は、中心の円の塗り分け方に等しいことになります。
背景の塗り分け方
この絵には4か所の背景が存在します(下図①-④)。

ここで、4か所の背景を異なる4色で塗り分ける方法は 4! = 24通り、4か所の背景をすべて同じ色で塗る方法は 4通り (赤・青・白・金)存在するため、これらを合わせると背景の塗り分け方は 24 + 4 = 28通り 存在することになりますね。
なお、4か所の背景を2色・3色で塗り分けることも考えられますが、これを認めると672通りという数字と辻褄があわなくなるので、どうやら認めていないようです。
トータルの塗り分け方
以上より、円の領域内の塗り分け方が24通り、背景の塗り分け方が28通り存在し、トータルでは24 x 28 = 672通りの塗り分けが存在することが確かめられました。
ちなみに、この全ての塗り分けを印刷した本が出版されているようです。

Gabriel Orozco: The Samurai Tree Invariants
- 作者: Gabriel Orozco
- 出版社/メーカー: Walther Konig
- 発売日: 2007/07/01
- メディア: ペーパーバック
- この商品を含むブログを見る
生成的な視点から
ここまではガブリエル・オロスコによって描かれたサムライ・ツリーを分析しましたが、自分でオリジナルなサムライ・ツリーを生成するにはどうしたらよいでしょうか? ジェネラティブ・アートに興味を持つ*2身としては、とても気になります。
輪郭については、中心に小さめの円を配置し、そこから上下左右にランダムな大きさの円をつなげていけばよいでしょう。その際には、円どうしの干渉や枠のサイズを考慮する必要がありそうですね。
塗り分けについては、672通りの計算のときのように考え、中心の円をまず塗り分け、そこから「ルール」にしたがって塗り分けていけばよさそうです。
そのうちプログラムを描いてつくってみたいですね。