国旗には何色がよく使われているのか? - Pythonで色相の頻度分布を調べてみる
概要
Wikipediaを見ると206カ国の国旗が掲載されていますが、国旗にはどのような色が使われる傾向にあるのでしょうか。
ぱっと見では原色系の派手な色が多いような…?
国旗の一覧 - Wikipedia
実際はどうなのか、画像処理によって調べてみました。
具体的には、
- Python + Beautiful Soupによるスクレイピングで国旗画像を取得
- Python + OpenCVによる画像処理で色相の頻度分布を計算
- Javascript + Canvasによって頻度分布を分かりやすく可視化
ということを行います。
目次:
- 概要
- 方法・結果
- 基本的な方針
- 色相
- 頻度の定義
- Pythonによるスクレイピング
- OpenCVによる画像処理
- Javascriptによる頻度の可視化
- 基本的な方針
- 考察
- ソースコード
- Python(スクレイピング・OpenCV・ファイル出力)
- HTML, Javascript(可視化)
- おわりに
- 関連

電子工作用の熱収縮チューブで靴ひもを短くする
経緯
靴ひもが長すぎて困っていました。
地面に接触するのですぐにほどけるし、トイレ等の床に触れたひもを触るのは不潔感があります。
切って短くすればいいのですが、先端部をどう処理するのだろうか?
…と思って調べていたところ、こんな商品を発見しました。ちくわ状のチューブにひもを通し、熱によってチューブを固めるというものです。

- 出版社/メーカー: 川村製紐
- メディア: Tools & Hardware
- この商品を含むブログを見る
でも割高! そうだ、電子工作用の熱収縮チューブ*1(¥100)なら手元にある!
というわけで、電子工作用の熱収縮チューブで靴ひもの端部を処理してみました。真似する方は自己責任でお願いします。
*1:ケーブル等で金属部分が露出している部分を絶縁するために用いられるもの
3Dプリンタに使われるSTLファイルを地理院地図3Dと併せてマスターする
目次

はじめに
ネットから3Dプリントが可能*1になるなど、ふつうの人でも3Dプリンタを使ったものづくりが可能になりつつあります。その際には、
- 3次元設計ソフトなどでデザインする
- その3次元データを3Dプリンタに送り、プリントする
という流れを経ることになると思うのですが、この「3次元データ」にはどのようにして形状の情報が埋め込まれているのでしょうか? それを理解してしまえば、例えば3次元設計ソフトを使わずに自分のプログラムから(数式などに基づいて)3次元データを吐き出させることが可能になり、人生が楽しくなりますね。
DNA上の塩基配列とアミノ酸の対応関係を木構造で表現する
目次
はじめに
前提知識
われわれの体はタンパク質で出来ており、タンパク質はアミノ酸がたくさんつながることによって構成されています。そのアミノ酸の配列というのがどう決まるかというと、DNA上のA(アデニン)・T(チミン)・G(グアニン)・C(シトシン)の並び方から定まります。
ではDNA上のATGCの配列とアミノ酸はどのように対応付けられるのでしょうか?
物理学者のジョージ・ガモフは、ATGCからなる三文字の文字列(ATC, GCAなど)がそれぞれアミノ酸に対応していると考えました。なぜなら、ATGCの4種類の文字をn文字並べた場合4のn乗通りの文字列が存在しますが、n=2では4^2=16、n=3では4^3=64となり、アミノ酸が20種類であることを考えるとn=3文字の場合が最も妥当であると予想されるからです。
その後ガモフの正しさが証明され、DNA上のATGCからなる3文字の塩基配列が20種類のアミノ酸を冗長にコードしていることが分かりました。
(もう少しちゃんとした説明↓)
コドン - Wikipedia
精巧な組木「千鳥格子」をPC上で再現し、実際に作ってみる
はじめに
隈研吾氏の著作「小さな建築」を読みました。くま氏は新国立競技場仕切り直しコンペに参加を予定している*1建築家で、木材を使うなど「和」をイメージしたデザインが特徴的だそうです。

- 作者: 隈研吾
- 出版社/メーカー: 岩波書店
- 発売日: 2013/01/23
- メディア: 新書
- クリック: 8回
- この商品を含むブログ (13件) を見る
この本に「千鳥格子」という玩具が紹介されていました。詳細・画像は以下の引用・リンクをご覧ください。
「千鳥」という飛騨高山に昔からある組み木のような木製の玩具で、飛騨高山の街ではビニールの袋に入って500円くらいで売っているものなのですが、これがとてもよくできている。切り欠きが施されている三種類の木の棒を組んでひねると、釘がなくとも固定される立体的な積み木なのです。
なんだか面白そうです。
で、書籍「小さな建築」や上記のリンクに「千鳥格子」の組立図が掲載されているのですが、小さくてよく分からない…。これを分かるようにするのが今日のテーマです。
目次
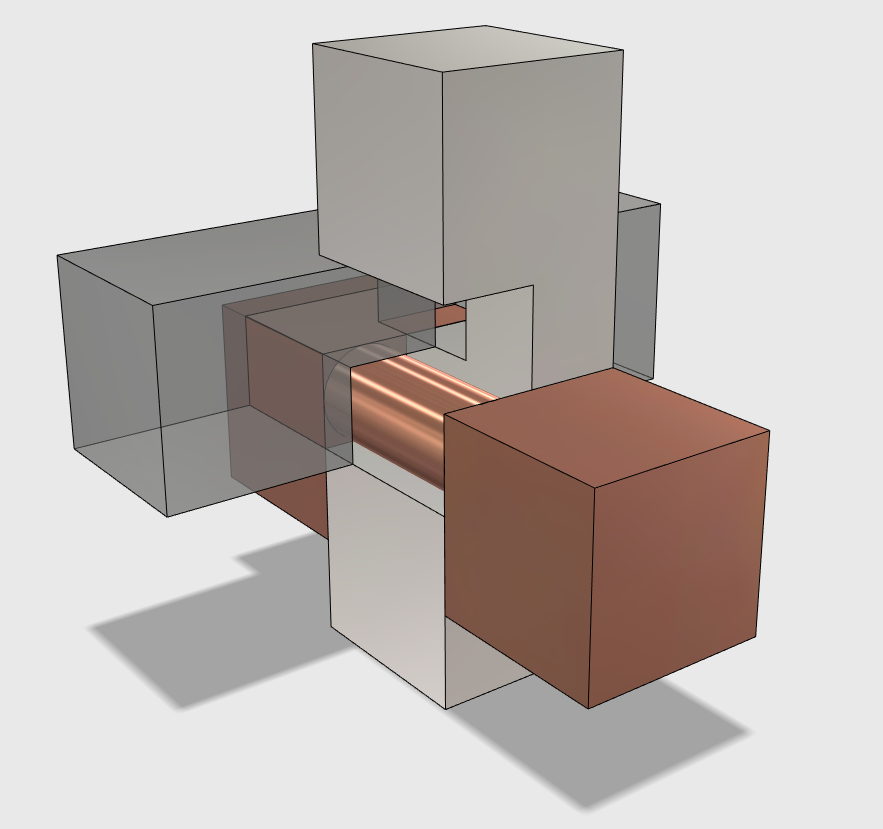
- 3次元CAD(立体作成ソフト)による「千鳥格子」の再現
- 部品の形状
- 組合せ方
- 発泡スチロールによる試作
- 材料・加工法
- 画像
- おわりに
- その他三次元っぽい記事
*1:(2015年10月現在) 【新国立競技場】コンペに竹中・清水・大林が連合 大成は設計者に隈氏 - 産経ニュース
ハンバーガーとしてのカントール集合と、L-systemによる表現
この記事では、ハンバーガーとの対比により、カントール集合というフラクタルの一種を理解することを目指します。パンの塊に対して「ある簡単な操作」を無限回繰り返してゆくと、無限枚のパンが含まれるにもかかわらずパンの割合が0%という奇妙なハンバーガーが出来上がるのです。
さらに、この奇妙なハンバーガーをL-systemという一種の形式言語によって記述したり、問題をビッグマックに拡張したりもします。
目次
続きを読む某エンブレムをフラクタル化して無限にズームし、面積も求める
はじめに
東京オリンピックのエンブレムについて一悶着あったようですね。詳しいことは知りませんが、エンブレムの面積を計算している方がいて人生楽しそうだなと感じました。
この姿勢を見習い、本記事ではエンブレムをフラクタルっぽくしてみることにします。さらに、フラクタル図形は無限に細かい形状といえるので、HTML5のCanvasを用いて無限にズームし続けるアニメーションを製作します。そして最後に、こうしてできたフラクタル図形の面積を計算して締め括ることとします。
参考:フラクタル図形とは、図形の部分と全体が自己相似になっているようなマトリョーシカ的図形のことです↓
フラクタル - Wikipedia