3Dプリンタに使われるSTLファイルを地理院地図3Dと併せてマスターする
目次

はじめに
ネットから3Dプリントが可能*1になるなど、ふつうの人でも3Dプリンタを使ったものづくりが可能になりつつあります。その際には、
- 3次元設計ソフトなどでデザインする
- その3次元データを3Dプリンタに送り、プリントする
という流れを経ることになると思うのですが、この「3次元データ」にはどのようにして形状の情報が埋め込まれているのでしょうか? それを理解してしまえば、例えば3次元設計ソフトを使わずに自分のプログラムから(数式などに基づいて)3次元データを吐き出させることが可能になり、人生が楽しくなりますね。
ヒマワリと黄金比の関係をインタラクティブなアニメーションにする【Javascript】【Canvas】
はじめに
先日、『数学で生命の謎を解く』という本を読みました。この本の第4章「花の中にみつかるフィボナッチ」には、植物の葉・ヒマワリの種子・パイナップルの模様がフィボナッチ数列*1と深く関わっていることが説明されています。
「花の中のフィボナッチ」は数学と生命科学の関係を述べた文章に必ずと言っていいほど登場する鉄板ネタなのですが、本書には以下のような興味深いモデル(フォーゲルのモデル)が紹介されていました。
1979年にミュンヘン工業大学のヘルムート・フォーゲルが、ヒマワリの種子が取る幾何の単純な数学的表現を考え、それを使って、そのような配置に黄金角が特別適している理由を説明した。*2
フォーゲルのモデルでは、n番目の原基は137.5度のn倍の角度に置かれ、中心からの距離はnの平方根に比例する。これらの二つの数によって原基の位置が決定し、ホフマイスターの生長らせんは、中心から外側へ行くにつれ巻き方がきつくなる、フェルマーらせんと呼ばれるものであることが分かる。
フォーゲルはこのモデルを用いて、同じ生長らせんを使いながらも黄金角137.5度からわずかにずらしたときに、花頭がどうなるかを導き出した。結果は、(中略)黄金角を使ったときにだけ、種子は隙間や重なりを作らずにびっしり並ぶのだ。角度を10分の1度変えただけで、パターンが壊れて一種類のらせんだけになり、種子のあいだに隙間ができてしまう。
『数学で生命の謎を解く』p59 (太字は引用者による)
これを自分で実装し、アニメーションにしてみました!
*2:Vogel, Helmut. "A better way to construct the sunflower head." Mathematical biosciences 44.3 (1979): 179-189.
DNA上の塩基配列とアミノ酸の対応関係を木構造で表現する
目次
はじめに
前提知識
われわれの体はタンパク質で出来ており、タンパク質はアミノ酸がたくさんつながることによって構成されています。そのアミノ酸の配列というのがどう決まるかというと、DNA上のA(アデニン)・T(チミン)・G(グアニン)・C(シトシン)の並び方から定まります。
ではDNA上のATGCの配列とアミノ酸はどのように対応付けられるのでしょうか?
物理学者のジョージ・ガモフは、ATGCからなる三文字の文字列(ATC, GCAなど)がそれぞれアミノ酸に対応していると考えました。なぜなら、ATGCの4種類の文字をn文字並べた場合4のn乗通りの文字列が存在しますが、n=2では4^2=16、n=3では4^3=64となり、アミノ酸が20種類であることを考えるとn=3文字の場合が最も妥当であると予想されるからです。
その後ガモフの正しさが証明され、DNA上のATGCからなる3文字の塩基配列が20種類のアミノ酸を冗長にコードしていることが分かりました。
(もう少しちゃんとした説明↓)
コドン - Wikipedia
精巧な組木「千鳥格子」をPC上で再現し、実際に作ってみる
はじめに
隈研吾氏の著作「小さな建築」を読みました。くま氏は新国立競技場仕切り直しコンペに参加を予定している*1建築家で、木材を使うなど「和」をイメージしたデザインが特徴的だそうです。

- 作者: 隈研吾
- 出版社/メーカー: 岩波書店
- 発売日: 2013/01/23
- メディア: 新書
- クリック: 8回
- この商品を含むブログ (13件) を見る
この本に「千鳥格子」という玩具が紹介されていました。詳細・画像は以下の引用・リンクをご覧ください。
「千鳥」という飛騨高山に昔からある組み木のような木製の玩具で、飛騨高山の街ではビニールの袋に入って500円くらいで売っているものなのですが、これがとてもよくできている。切り欠きが施されている三種類の木の棒を組んでひねると、釘がなくとも固定される立体的な積み木なのです。
なんだか面白そうです。
で、書籍「小さな建築」や上記のリンクに「千鳥格子」の組立図が掲載されているのですが、小さくてよく分からない…。これを分かるようにするのが今日のテーマです。
目次
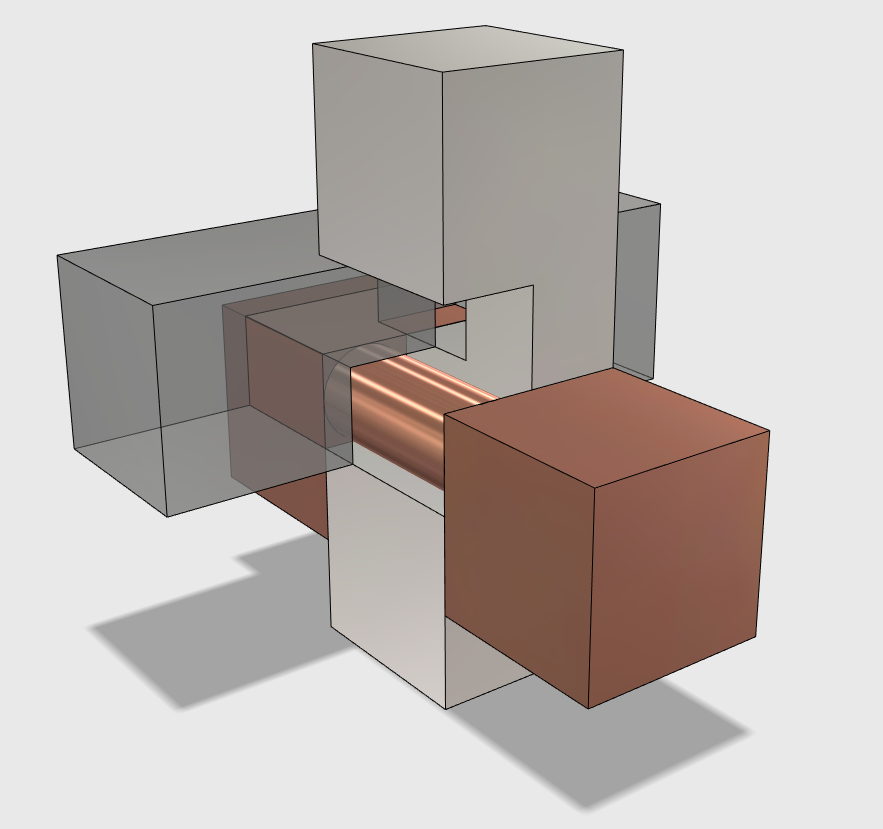
- 3次元CAD(立体作成ソフト)による「千鳥格子」の再現
- 部品の形状
- 組合せ方
- 発泡スチロールによる試作
- 材料・加工法
- 画像
- おわりに
- その他三次元っぽい記事
*1:(2015年10月現在) 【新国立競技場】コンペに竹中・清水・大林が連合 大成は設計者に隈氏 - 産経ニュース
ハンバーガーとしてのカントール集合と、L-systemによる表現
この記事では、ハンバーガーとの対比により、カントール集合というフラクタルの一種を理解することを目指します。パンの塊に対して「ある簡単な操作」を無限回繰り返してゆくと、無限枚のパンが含まれるにもかかわらずパンの割合が0%という奇妙なハンバーガーが出来上がるのです。
さらに、この奇妙なハンバーガーをL-systemという一種の形式言語によって記述したり、問題をビッグマックに拡張したりもします。
目次
続きを読む最も偉大で最ももの悲しい『ドン・キホーテ』ほか - 2015年9月に読んだ本まとめ
今週のお題「人生に影響を与えた1冊」
はじめに
9月に読んだ19冊を記しておきます。涼しくなったおかげで結構読めました。
なかでも『ドン・キホーテ』は名作です。あのドストエフスキーが
「人間の魂の最も深い、最も不思議な一面が、人の心の洞察者である偉大な詩人によって、ここに見事にえぐり出されている」
「人類の天才によって作られたあらゆる書物の中で、最も偉大で最ももの悲しいこの書物」
と評したとのこと。
ドン・キホーテ - Wikipedia
以下では今月読んだ本を「小説(海外)」「小説(国内)」「理系っぽい本」「その他(エッセイ・教養・音楽等)」の4つに分類しました。
各本について、タイトル・リンク・読書メーターに書いた感想(一部追加・修正あり・非ですます調)の順に記します。↓↓↓